福西です。初回は、汎用ロジック回路というものを使って、論理式を考えました。
(74HC00の外観)
ロジック回路には、色々と種類があるのですが、今日はいちばん基本的な、NOT回路(74hc04)と、NAND回路(74hc00)を紹介しました。この中には、FETを使って構成されたスイッチ回路が複数入っています。そして足の説明をしたあと、実際にLEDを付けて動作を確認しました。
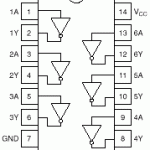
(74hc04の回路図)
74hc04も、74hc00も、7番ピンがGNDで、14番ピンがVCCであることは共通です。ただしそのあとの入力ピンと出力ピンの配置が異なります。注意としては、使用していない入力ピンはGNDに落として、誤作動を防いでおくことです。
74hc04は、1番ピンの入力を、反転させて2番ピンに出力します。(それと同じ回路が6つ入っています)。回路図の矢印の先にある○印が、反転(NOT)の意味です。
論理図は以下の通りです
NOT回路の論理
入力 出力
0 → 1
1 → 0
もし反転させた出力が不便で、0→0、1→1と対応させたいときは、2番ピンの出力をまた入力とみなして、3番ピンに入れ直すことで、4番ピンからそのような出力が得られます。それならば最初から何もしなくていいようにも思いますが、こういうのをバッファといいます。パソコンを自作する人なら、よく聞く名前かもしれません。誤作動から信号を守る時によく使われます。(バッファは緩衝という意味です)。
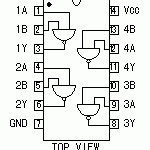
(74hc00の回路図)
74hc00は、1番ピンと2番ピンの入力から、以下の論理を3番ピンに出力します。(それと同じ回路が計4つ入っています)
NAND回路の論理
入力1 入力2 出力
0 0 → 1
0 1 → 1
1 0 → 1
1 1 → 0
入力が二つあるので、さっきのNOT回路よりも複雑になっています。意味は、入力が一つでも0なら1を出力し、入力が二つとも1の時に初めて0になります。
NANDというのは、NOT+ANDつまり「ANDを否定した」という意味です。AND回路より複雑な感じがしますが、いちばん基本的なロジック回路とされています。実際、このNAND回路から、他にOR回路、AND回路を作ることができます。(またAND回路とNOT回路で、NAND回路を作ることができます)。
さて、74hc00には、NAND回路が4つ入っているわけですが、それを3つ使って、最後にAND回路を作ってみることを考えました。
AND回路の論理
入力1 入力2 出力
0 × 0 → 0
0 × 1 → 0
1 × 0 → 0
1 × 1 → 1
(ORが実は足し算で、ANDは掛け算となります)
二つの入力から、上の関係の出力を取り出せばいいのですが、それには、ヒントとしては、NAND回路の出力を、再び別のNAND回路の入力に入れ直します。また、入力線もただ2本考えるのではできなくて、4本にして、それらを2本ずつ束ねます。さて、それはどういうことなのでしょうか?ということを考えてもらいました。
この論理回路を使えば、動くものの実用としては、ライントレーサーが作れるのですが、私が「今まで地味なことばかりしてきたので、今年は動くものを作りたいなあ」と言うと、A君が「いや、基本も結構難しいですよ」と言ってくれました。それで、なるほど、と私の方がかえってそう思いました。