
福西です。
『図形(下)』(小和田正・田島信夫、さ・え・ら書房)を読んでいます。
p24~29「コンパスの使い方」「円と三角形」を読みました。

コンパスは、長さをコピーする道具であることを確認しました。
私たちの使うものさしには、目盛りのあることが普通です。でも昔のものさしは、ただまっすぐな線を引くための道具でした。そこで、単位(=1)となる長さを、針と針ではさんでコピーする、コンパスが活躍します。
コンパスとものさしを使うと、「作図できる数」という問題を考えることができます。
2(の長さの線分)は、コンパスの半径を1とすると、直径として描けます。
3(の長さの線分)は、先の2の長さをコンパスで移し、1に加えると描けます。
コンパスは、ただ図を描くだけでなく、数(代数)とも関係があることを知ってもらえると幸いです。
また、ターレスの定理を、テキストの説明に沿って、証明しました。
ターレスの定理とは、三角形の2点(下の図のA、C)を直径の両端とし、もう1点(B)を円周上の好きな場所(A、C以外)にとるとき、必ず直角三角形ができるというものです。円と三角形を結ぶ、大変美しい定理です。
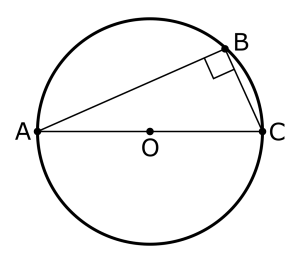
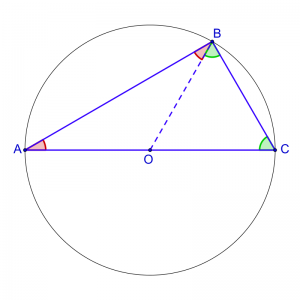
その証明では、二等辺三角形が活躍することを見ました。
残りの時間は、パズルのプリントをしました。