福西です。ここ数週間分の近況の報告です。
Mさんは「連立方程式の解法」を、M君は「一次関数とグラフ」のところを、R君は「文字式の復習」とM君と同じところをしています。
Mさん
連立方程式には、代入法と消去法とがあり、それを順番に習いますが、実は代入法は(連立方程式を解くためには)それほど重要ではありません。ですので、代入法か消去法かで迷う義理はなく、「要するに文字を一つ消しさえすればいいんだ」と大きく理解しておけばいいでしょう。
(むしろここでの扱われ方は、代入の「応用」問題といった感があります。そうではなく、代入が切実になるのは、私が思うに、方程式が関数の話になってからです)。
ですので、私のお勧めは、「いつでも消去法」です。よくよく考えれば、1つ目の文字を消去法で決定したあと、二つ目のそれは代入法で決定していることになるので、そうやっても代入の話を忘れる事はないと思います。
さて、Mちゃんは、この消去法の「係数をそろえる」ということに、だいぶ自信を持ってくれていました。たとえば、そろえたい文字がxだとすれば、二つの式の中に2xと3xが見えれば、6xにすればよいことをぱっと思いついてくれます。そして3倍と2倍をそれぞれ実行してくれます。このとき、右辺(=の右側)の数字にもきちんと同じ数をかけてくれます。その調子です。
また一方で、時折、癖として見られたことがあります。それは、文字をそろえた後、6xと-6xというような異符号の時に、つい+同士の時と同じように引き合ってしまうことでした。それを「足せば消える」というように練習してもらいました。
きのうは、係数が小数の場合と分数の場合を見ました。
1)0.4x+0.6y=0.1 → 10倍すればO.K.
2)x/4+y/6=1 → 12倍すれば(4と6の最小公倍数だけかければ)O.K. このとき、右辺の1にも12倍し忘れないことがポイント。
この作業さえ間に挟めば、あとは今までどおり話が進められます。
ここで確認した自信は、他の方面でも足がかりとなり、波及効果がありますので、ぜひ大事にしてください。
M君、R君
一次関数の問題では、「分からない」と言う前に、とにかくできることを実行します。それも、たった一つだけのことです。
一次関数の形を、
y=ax+b
とおくことです。
これは、どんな時でも真っ先にして欲しいことです。これをまず、解答用紙の一番最初に書くこと。それさえすれば、あとは自動的に解けます。なので、上の式を書くことは、「おまじない」や「呪文」だと思ってもらってもいいぐらいです。とにかく唱えてください(笑)
一次関数の問題は、とどのつまり、
1)y=ax+bを書く(ここが一番重要!)
2)二つのヒントを集める
3)係数a,bを決定する
この流れに集約されます。
2)のヒントには、いくつか組み合わせがありますが、しかし無限にあるわけでも、莫大に多いわけでもなくて、たった2~3×2~3の数パターンだけです。ですので、かなり狭い有限の話で、鳥瞰するのはたやすいです。一方、一次関数の問題を難しいと感じる人は、これが「途方もなく広く」見えてしまっている傾向があります。M君はそれが「有限」に見えているようで、自信を持って淡々と問題を解いてくれていました。一方、R君にはまだ「無限に近い」と感じられているようで、実際に問題を解いて、そこをつめてもらいました。(いずれにせよ、問題をしてもらうことに変わりはありませんが^^)
問い:次の一次関数の形を求めよ。
a)傾きが2/3で、切片が1/3。
b)y=(2/3)x+1に平行で、y軸にy=1/3で交わる。
c)点(1,1)を通って、x軸にx=-1/2で交わる。
d)点(1,1)と点(2,5/3)を通る。
a)は、一番簡単です。y=ax+bのaが傾き。bが切片のことです。なので、
1)まずy=ax+bと書く
2)a=2/3、b=1/3を代入
3)y=2/3+1/3。
b)も、実は単にa)の言い換えです。平行というのは、傾きが同じということです。ということはa=2/3というヒントに他なりません。そしてy軸に交わるということは、その時のxの値は0ということです。つまり「y軸に」は「切片が」の言い換えです。ですので、これもa)と同様に((2)の手間が同じなので)、
1)まずy=ax+bと書く
2)a=2/3、b=1/3を代入
3)y=2/3+1/3。
c)も、やはり最初にy=ax+bとまず書いておきます。そして、x軸に交わるということは、その時のyの値は0ということです。つまり「x軸で-1/2を通る」は「点(x,y)=(-1/2,0)を通る」の言い換えです。
1)まずy=ax+bと書く
2)(x,y)=(1,1)を代入→1=a+b
(x,y)=(-1/2,0)を代入→0=-(1/2)a+b
3)連立方程式を解いて、y=2/3+1/3。
d)はある意味、一番頭を使わなくてもいい形式です。要するに、y=ax+bに2回代入すれば、あとはただの連立方程式になります。ですのでこれもc)と同様に((2)の手間が同じなので)、
1)まずy=ax+bと書く
2)(x,y)=(1,1)を代入→1=a+b
(x,y)=(2,5/3)を代入→5/3=2a+b
3)連立方程式を解いて、y=2/3+1/3。
このように、とにかく最初にy=ax+bと書けば、「一次式の形を求めよ」という問題は、単なる「a,bを求めよ」という計算になってしまうのがミソです。
最後にもう一つ。M君が「お父さんと考えてここまでは分かったけれど、ここからがどうしても分からない」と悩んでいる問題を見せにきてくれたので、それを一緒に考えました。
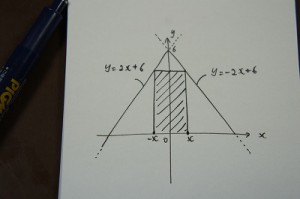
問い(改題):図のように長方形の1点を表すxが動くとき、斜線部が正方形になるという。その時の面積はいくらか。
これは正方形というのが一つ目のヒント、そしてy=-2x+6というのが二つ目のヒントです。
「まず、底辺の長さはx+xで2xになるのは分かる?」
というと、
「うん、それは分かる」
とM君。
「じゃあ今、正方形なので、その時の高さは、いくらになる?」
と聞くと、しばらく考えてから、
「2x?」
とM君。
「さて、正方形の高さには、一方でyという言い方があった。ということは、y=2x。これは分かる?」
と、そこで、
「ああ、そっか!」
とうなずくM君。(ここがM君の分からなかったところでした)。
「OK? なら、正方形の高さを表す関数が、y=-2x+6で与えられているんだから、そのyに2xを代入したら、どうなる?」
と聞くと、
「そうか、そういうことか!」
と何度もうなずくM君。
「というわけで、2x=-2x+6。xは?」
「えーと、4x=6やから…x=3/2?」
「正解。じゃあ、yは?」
「3」
「面積は?」
「9。正方形だから…って、おお、できた~!」
「じゃあ、あとは、さっきのことを、今度は自分で納得しながら答に書いてごらん」
というわけで、この問題は、本質的に「代入」を考えるという一例でした。