浅野です。
おもしろくてためになる入試問題を集めています。
次の文章は、ある条件を満たすものが存在することを証明する際に、よく使われる「鳩の巣原理」(または抽出し論法とも言う)を説明したものである:
m 個のものが、n 個の箱にどのように分配されても,m > n であれば,2 個以上のものが入っている箱が少なくとも 1 つは存在する。このことを鳩の巣原理という。
たとえば、3 つの整数が与えられたとき,このうちの少なくとも 2 つはともに偶数であるか,又はともに奇数である。なぜならば、3 つの整数を偶数であるものと奇数であるものとの 2 組に分けると、鳩の巣原理(m = 3, n = 2)により,偶数の組または奇数の組に 2 つ以上の整数が入っているからである。
この原理を用いて、次の命題 (1)、(2) が成り立つことを証明せよ。ただし,証明はこの原理をどのように使ったかがわかるようにせよ。
(1) 1 辺の長さが 2 の正三角形の内部に、任意に 5 個の点を取ったとき、そのうちの 2 点で、距離が 1 より小さいものが少なくとも 1 組存在する。
(2) 座標空間で、その座標がすべて整数であるような点を格子点という。座標空間に 9 個の格子点が与えられたとき、そのうちの 2 点で、中点がまた格子点であるものが少なくとも 1 組存在する。(広島大)
これはおもしろいです。私が作った解答を以下に載せておきます。
(1)
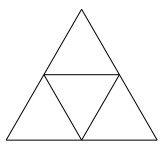
上図のように、1 辺の長さが 2 の正三角形を、1 辺の長さが 1 の正三角形 4 つにわける。鳩の巣原理(m = 5, n = 4)により、4 つある 1 辺の長さが 1 の正三角形の少なくとも 1 つについて、5 個の点のうち 2 つ以上の点がその内部または周上(頂点を除く)に入っている。1 辺の長さが 1 の正三角形の内部または周上(頂点を除く)にある 2 点間の距離は 1 より小さい。よって、1 辺の長さが 2 の正三角形の内部に、任意に 5 個の点を取ったとき、そのうちの 2 点で、距離が 1 より小さいものが少なくとも 1 組存在する。
(2)
座標空間内の格子点 2 点 (x1, y1, z1), (x2, y2, z2) を考える。この 2 点の中点は ((x1 + x2)/2, (y1 + y2)/2, (z1 + z2)/2) である。この中点が格子点となるためには、x1 + x2, y1 + y2, z1 + z2 のすべてが偶数となればよい。つまり、x1 と x2、y1と y2、z1 と z2 の偶奇がすべて一致すればよい。座標空間内の格子点の x, y, z 座標の偶奇のあり方は 2^3 = 8 通りである。よって、鳩の巣原理(m = 9, n = 8)により、8 通りある偶奇のあり方の少なくとも 1 つに、9 個の格子点のうち 2 点以上があてはまる。以上より、座標空間に 9 個の格子点が与えられたとき、そのうちの 2 点で、中点がまた格子点であるものが少なくとも 1 組存在する。