
福西です。
以前、Eさんが複素数を取り上げてくれたので、それの興味を喚起する教材について書いておきます。(なかば講師用メモ)
1)2次方程式の複素数解の可視化
2次方程式は判別式D<0の場合は、実数の範囲では「解なし」となりますが、複素数の範囲では「異なる2つの複素数解」があります。
ただし「存在する」と言いながら、複素数解はxy座標のグラフでは見えません。そこでそれを「何とか見たい」という需要にこたえたのが、以下の文献です(pdf)。
複素数平面上における 2 次方程式の虚数解の存在位置について-3Dgrapesを活用して-
この文献にしたがって、以下のサイトにある「3D-GRAPES 1.73」「3D GRAPES 1.76」(2021年現在)というソフトでお絵かきします。
1)grps3d173.zip(2.5MB) grps3d176.zip(3.0MB)というのをダウンロードします。
2)grapes3D.exeを実行し、立ち上がった画面の右欄に、下記の式を入力します。
i)曲面に
R (u,v,au^2-av^2+bu+c)
曲線に
P (u,0,au^2+bu+c)
Q (-b/2a,v,-av^2-b^2/4a+c)
変数uとvの範囲は、-10から10など適当に決めます。
ii)点に
A ((-b-Sqrt(b^2-4ac))/2a,0,0)
B ((-b+Sqrt(b^2-4ac))/2a,0,0)
S (-b/2a,-Sqrt(-b^2+4ac)/2a,0)
T (-b/2a,-Sqrt(-b^2+4ac)/2a,0)
iii)パラメーターに
a=1
b=-2
c=2
お疲れさまでした。
そして、このcを小さくすると実数解、大きくすると複素数解が現れます。
画面を90°ずつ回すと、「虚と実」の世界を行き来できます。このように視野を複素数にまで広げると、実数の世界で見ているもの(たとえば二次関数のグラフ)がほんの「切り口の一つ」にすぎないということが分かって面白いと思います。

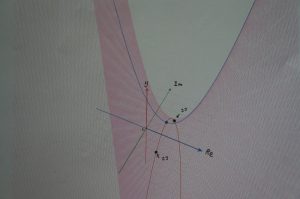
2次方程式の解は、2次関数y=ax2+bx+cとx軸(y=0)との交点のこと。
左図)x軸(青線)に交わらない時は「解なし」
央図)定義域をx軸から複素平面(青線と緑線で張る面)に拡張
右図)ピンク色の鞍状の曲面がy=ax2+bx+cの複素平面上での正体。
その切り口の一つ(赤いカーブ)と複素平面との交点が、「複素数解」。
2)マンデルブロー集合
複素平面といえば、「マンデルブロー集合」というのがあります。
以下の複素数の漸化式を考えます。
z0=0
zn+1=zn2+c
この漸化式の先が発散しない(|z∞|<∞である)ような複素数cの集合を、複素平面にプロットして現れる図形は、自分の中に自分と相似な形を持っています。それを顕微鏡で覗いていった一例が、以下の動画です。(色々な方がたくさんアップされています)
(マンデルブロ集合②-フラクタルフローラ)
いつか紹介しようと思っていたのですが、授業では時間が足りなかったので、こちらに記しておきます。