福西です。 今回は、第3巻の命題19と21を証明しました。(20は以前にしました)
命題3.21「弦を等しくする円周角はすべて等しい」
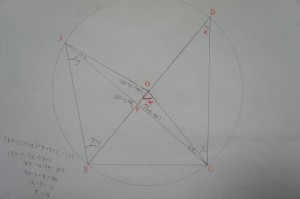
(すみません、かき間違えました。図では∠BCA*が90°となっていますが無視してください。以下ではそのことは使っていないので問題ありません)
有名な「円周角の定理」です。
さてR君は、命題を次のように読み替えてくれました。
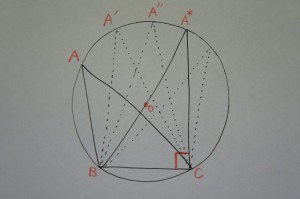
「すべての円周角(∠A、∠A’、∠A”…)は、∠A*と等しい」
と。
ここで、∠A*は、弦BCが直径すなわち中心を通るような円周角のことです。
こうすることで、以前に証明した命題3.20「円周角=中心角の半分」が使えるようになります。
すなわち、 ∠BCA*=xとすると、 ∠BOC=2xと表せます。
【R君の証明】
ADを中心を通る弦(直径)とする。∠BDC=x、そして任意の円周角を∠BAC=yとし、x=yを示す。
∠CAO=cとする。
OA=OCより、△OACは二等辺三角形なので、 ∠OCA=OAC=c。
OC=ODより、∠DCO=∠ODC(=BDC)=x。
OA=OBより、∠OBA=OAB=y+c。
∠POC=∠BOC=2∠BDC=2x。←ここで命題3.20を使えるようにしているのがR君のアイデアです。
∠APB=∠OPC=180°-(c+2x)。
よって、△PABについて、以下の式が成り立つ。
180°-(c+2x)+y+y+c=180°
これを整理すると、
y=xとなる。
これが示すべきことであった。