
福西です。
先週、Y君がつるかめ算を「あまり見たことがない」と言っていたので、今回は『てんびん算』を用意しました。
たとえば、こんな問題があるとします。
x+x+x=y+y
x+18=y+y
ここで、xとyの値を1ずつ変えせて解こうとすると大変です。
そこで、2つの式を見比べます。すると、1本目の式のy+yは、2本目の式でx+18に「両替できる」ということに気づきます。
つまり、こうです。
x+x+x=x+18
こうして未知数を1つにしてから、あとは等価な処理をしていきます。両方の天秤皿からxを1個ずつ取ります。
x+x=18
ここまでくれば、割り算に持っていくことができます。x=18÷2=9です。
よって、1本目の式から、y=27÷2=13.5。
今はyが小数になるようにわざと問題を作りましたが、この場合では、「値を1ずつ変化させる」という解き方がお手上げだということが分かると思います。
また一方で、Y君は、1本目のような式から、x>yというような大小関係を見抜いていました。不等号の情報はバチッと解が決まらないので敬遠されがちですが、役に立たないということは全然ありません。むしろそれが決め手となる場合もあります。少なくとも今は、問題のイメージがはっきりとつかみやすくなります。不等号の情報を集めることは、なかなか渋い着眼点であり、とても良い癖です。ぜひ自家薬篭中にしてください。
Rちゃんは、まずは学校のプリントをクリアしました。
![]()
のような式の整理の時、分母をそろえたあとの「/6」を書くのを忘れる癖があったので、「分子=」と最初に断わりを入れておくか、あるいは「/6」と書くことを指摘しました。
Rちゃんは計算を実行する際、少しずつの変化であっても、はしょらずに丁寧に一段ずつ書いてくれていました。それは「紛れがない」やり方で、とても良い癖です。
ほとんど同じ式を書き写すという作業は、一見無駄に思えます。しかし、「目の位置をほとんど動かさず、一つ上の式だけを常に見れていればいい」というのはメリットです。今その癖をつけておくと、後々(たとえば物理で式をフォローする時には)役立つと思います。
先の与式の場合、
与式
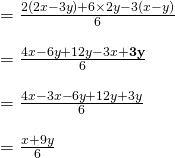
としてくれていました。xとyの順番を整理する作業を3段目に入れているのが丁寧だと思います。
計算間違いをしやすいポイントでは、1段目から2段目に移る際の-3(x-y)の後ろの方の3yです。これも忘れずに-×-で計算してくれていました。
あとの時間は、先週質問のあった、「奇数+奇数が偶数であることを証明せよ」といった形式の補充問題をしました。
まず1つ目のポイントは、題意にある自然数(整数)を文字で表すことです。たとえば2桁のそれは、10a+bといったように、すらすらと変換できれば○です。こっちはすんなりと腑に落ちていたようでした。
2つ目は、偶数や3の倍数であることを示すためには、2×(なんちゃらかんちゃら)や3×(なんちゃらかんちゃら)と、式を強引に指示されたその倍数でくくってしまうことです。こっちは慣れが必要な様子でしたので、その分の数をこなしてもらいました。