山の学校ゼミ（数学）（0131）（その１）

このクラスでは、『虚数の情緒』（吉田武著、東海大学出版会）を読んでいます。

その287ページに、「平方根が無理数であること」という話題で、プラトンの『テアイテトス』からの引用がされていました。そこで興味が湧いたので、調べてみました。

原文では次のようになっていました。（ペルセウス・プロジェクトより）

『テアイテトス』147dより
Θεαίτητος
περὶ δυνάμεών τι ἡμῖν Θεόδωρος ὅδε ἔγραφε, τῆς τε τρίποδος πέρι καὶ
πεντέποδος ἀποφαίνων ὅτι μήκει οὐ σύμμετροι τῇ ποδιαίᾳ, καὶ οὕτω
κατὰ μίαν ἑκάστην προαιρούμενος μέχρι τῆς ἑπτακαιδεκάποδος:
ἐν δὲ ταύτῃ πως ἐνέσχετο.　（…）

テアイテトス：
「テオドロス（テアイテトスの幾何学の先生）は私たちのためにそのように図を用いて描いた。3（平方）フィート（の面積の正方形）についても5（平方）フィート（のそれ）についても、（それらの１辺が）（単位）フィートで測れない（有理数で表せない）ことを示して、そのように17（平方）フィートについてまで、一つ一つ同様にして導出していった。で、そこで（√17で）どういうわけか彼は止めてしまった。…」（云々）
（訳は拙訳のため、不正確な点はご容赦下さい）

さて、なぜテオドロスが√17のところで止めてしまったのか、それについて数学史家たちが色々と考察をしているということを、『無理数の発見の歴史』というサイトで知りました。このサイトの記事は、はじめて知ることばかりで大変勉強になりました。

その記事によると、ファン・デル・ヴェルデンの本（『古代文明の数学』（日本評論社））で、テオドロスは（後にその名で呼ばれることになる）「ユークリッドの互除法」を使って証明したのではないか、という説が紹介されているそうです。

「ユークリッドの互除法」
１）２つの数を長方形の辺の長さで表します。ここでは、長い方を縦とします。
２）長方形の縦から横を可能な限り引き去ります。
３）あまった長さの辺を新しい長方形の横とし、前の長方形の横を今度は縦に取りかえます。
４）そのようにしてできた新しい長方形で、また、縦から横を引くことを考えます。
５）そしてまた新しい長方形を作ります。
６）これを順次、繰り返していきます。
７）もし、１）の長方形の辺の比が有理数である場合は、最後には必ず正方形で埋め尽くすことができ、１）の長方形全体もその正方形で分割して埋め尽くすことができます（つまり最後に求まった正方形の１辺が、１）の２つの数の最大公約数となります）。そして、その手順は有限となります。
８）もし、１）の長方形の辺の比が無理数である場合、手順は無限に繰り返されます。

たとえば、（縦、横）＝（48,31）の長方形を考えた場合、

（48,31）→（31,17）→（17,14）→（14,3）→（3,2）→（2,1）→（1,1）

となります。
（a,b）→（b,c）と、bの位置がコロコロと入れ替わるのは、「横を縦にクルッっとすること」（上の手順で言えば３））を意味しています。（こちらの図を参照）

さて、比が有理数であれば、ユークリッドの互除法は有限の手順で終わり、無理数であれば無限に続きます。後者が「平方根が無理数であること」の証明に使えるというわけです。

またそれには連分数展開で表現するのが都合がよいことを、そして連分数展開とユークリッドの互除法が等価であることも、先の『無理数の発見の歴史』の記事で知りました。（等価であることについては、そちらに詳しく説明がされていますので、ご覧ください）

さて、無理数をと表現します。（は整数部分、は小数部分）

無理数の中から整数部分（の部分）をしぼり出すと、それ以外の部分であるは、となります。 そしてと、分数の逆数で表すことで、分母の部分にという、1以上の数を作り出します。

（：整数部分、：小数部分）と表します。そうするとまた整数部分がしぼり出せます。 そして（いわば1の「残りかす」である）を、またと、分数の逆数で表すことで、>1を作り出します。

そうすることで、また整数部分（）がしぼり出せるようになります。

これを以下延々と繰り返していくと、{}と{}という二つ列が作れます。

そしてもし、ある時にがになることがあれば、そこからまた最初と同じ連分数が続くことになり、循環する、すなわち連分数展開が無限に続くことが言えます。

有理数ならばその連分数展開は有限で終わるはずなので、元の数は有理数ではないことが言える、という寸法です。

√17が無理数であることの証明

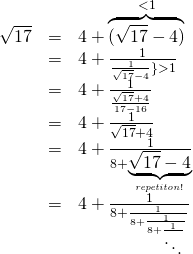
（最後の式は連分数の表記法です）

このように、１回逆数する作業をしただけで、連分数展開が循環することが示せ、早く証明が終わります。

『無理数の発見の歴史』によれば、ファン・デル・ヴェルデンの本に、これが「テオドロス先生が急に止めた」可能性の一つとして考えられるのではないか？（つまり証明が難しくてやめたのではなくて、むしろすぐに終わってしまったからではないか？）という説として紹介されている、とのことでした。（テオドロスはもちろん連分数は知らないので、それと等価な方法（ユークリッドの互除法）をもし使ったならばという話です）

同様に、「なぜテオドロス先生はそこから先へ続けなかったのか？」の可能性を探るために、√19の場合も見ておきます。

 

√19が無理数であることの証明

連分数展開を実行していくと、以下のようになります。

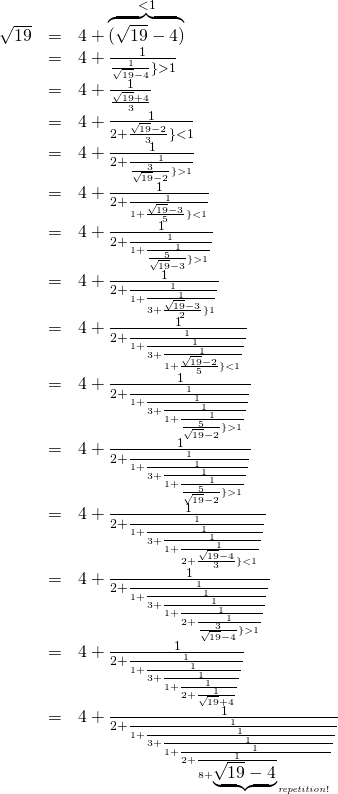
このように、循環節が6節もあり、大変面倒臭い！ことが見て取れます。