福西です。
先週「サッカーボールを作りたい!」という希望があったので、今回はそれを作りました。
サッカーボールは正5角形と正6角形の組み合わせで貼られた球面です。
そこで今、正5角形の枚数をx、正6角形の枚数をyとして、xとyを求めます。
正5角形は1枚につき頂点が5つあるので、x枚だと頂点は全部で5xあります。正6角形は6y。なので、もしそれら全部が球面の頂点だったとすると、5x+6yとなります。しかし実際には、面の貼り合せで頂点が重複するので、それよりも少ないことになります。
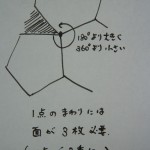
正5角形ないし正6角形を貼り合せると、一点のまわりには(2枚でも4枚でもなく)3枚の面が配置されることになります(上図)。これより1点を3重に数えていることが分かります。
よって、サッカーボールの本当の頂点の数は、
![]()
と求まります。
一方、線の方はというと、正5角形と正6角形全部の辺は5x+6yです。それを球面に貼り合せた時に、重複した回数で割ります。上図より、線を2重に数えていることが分かります。
よって、サッカーボールの本当の線の数は、
![]()
と求まります。
面は当然、
![]()
です。
これを前回の「オイラーの多面体定理」の式(点-線+面=2)に代入します。
すると、
![]()
となります。
(右辺の2には、実は「3次元-1」という意味があります。(球面を置いている空間の次元が3です。これが平面なら左辺は2-1=1となります。))
これを解くと、
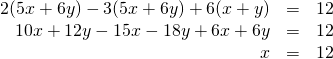
(不思議とyの項は12-18+6=0で消え、xの項が10-15+6=1でxだけ残ります。)
yの項が消えるということは、条件を追加して考えなければyを求めることはできません。
これは授業では触れませんでしたが、実は単に立体を作るだけならば、yは任意のパラメーターで、それに応じて色々な形を取り得ます。
そこで「正5角形が隣り合わない」という条件を加えます。そうすれば、yは任意ではなくなります。さらに「回転対称」という条件を加えます。これがサッカーボールになる条件です。また後者の(球状になるための)条件を外せば、楕円形のカプセルや、細長い風船(長さがいろいろ変る)のような形もできます。
ただし正5角形については、どんな形状であっても必ず12枚必要だというのが、上の式から出てきた結論です。
ちなみに正5角形は、筒の両端を閉じるための「ふた」として、その両端に6枚ずつ使うことになります。
下の写真で、K君が作っているこの正5角形6枚(5枚+1枚)による形が、ちょうどその「ふた」です。(黄緑が正5角形)
今は球にいちばん近い形、サッカーボールを考えているので、筒が一番短い状態、つまり「ふた」を最短で2枚貼り合せた形になります。
するとサッカーボールは、次のような、正6角形を間に1枚挟んで、正5角形が交互に現れるパターンで(どの方向から見ても)構成されていることが分かります。
さっきはオイラーの多面体定理から、正5角形の枚数が12だと分かりましたが、正6角形の枚数は不明でした。
そこで上の絵をもとに、サッカーボールの場合の正6角形の枚数を考えてみます。(「正5角形は隣り合わない」という条件を付加しています)
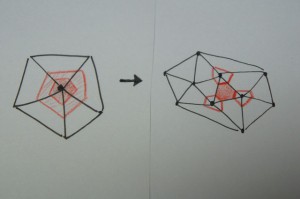
まず、赤枠で囲んだ正5角形のまわりに、正6角形は5枚あります(正5角形の辺は5つなので)。そして正5角形は12枚ありました。もしサッカーボールに使う正6角形がこれ全部だとすると、5×12=60枚になるはずです。
しかし当然重複している面があります。
それはどうやって考えるかと言うと、上の絵で赤い点を打った正6角形に注目します。
このまわりには、正5角形が3つあります。(サッカーボールの場合、正5角形は1つ飛ばしに現れるので)
つまり、こっちで見れば、正6角形1枚のために、正5角形を3枚使っていることになります。
ということは、さっきの計算は、3重に数えていたことになります。
なので、
5×12÷3=20。
これが正6角形の数です。
よって、サッカーボールに必要な面の数は、
正5角形12枚、
正6角形20枚
だと分かりました。
【補足】
実は、サッカーボールは、正20面体から作ることができます。
ボールに使うなら、「正20面体をもっと転がる形にしよう」という発想から、頂点をすりつぶすことを考えます。
それをしていくと、点から正5角形が現れます。(なぜなら1点には5枚の正三角形が貼り付いているから)。
そしてまわりの正三角形の様子を合わせてみると、正5角形に挟まれた部分に、正6角形が浮かび上がってきます。
(正20面体の点を正5角形に広げていくと、正3角形の面がだんだん正6角形へと変化していきます)
さて、正20面体の頂点の数は12あります。なのでそのまま、それが正5角形の枚数になります。また、正20面体の面の数は20だったので、それがそのまま正6角形の枚数になります。
よって、正20面体から作った立体(すなわちサッカーボール)は、
正5角形12枚、
正6角形20枚
だと分かりました。
サッカーボールは32面体なんですね。
(でも「正」じゃないというのがミソです)