山の学校ゼミ(数学）（0131）（その２）

前回の記事の、ユークリッドの互除法と、連分数についての補足です。

有理数の4/3は、1次方程式3x=4の解ですが、それは小数展開だと1.333…と循環する無限で表されます。しかし、連分数展開ではそれが有限で表されます。

 

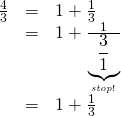
これはある意味そのままという気もします。なので、もう少し複雑な場合、たとえば31x=48（31と48は互いに素）で考えると、次のようになります。

 

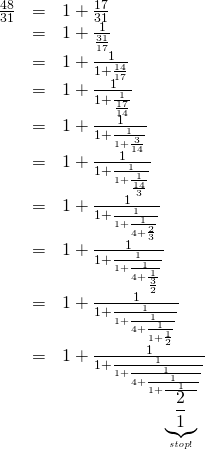
一方、無理数の√3は、2次方程式x²=3の解（の一つ）ですが、これは小数展開では1.7320508075…と、循環しない無限で表されます。

けれどもそれが連分数展開では、その１で示したように、循環する無限で表されます。

（ユークリッドの互除法で言うなら、長方形の隅がいつまでたっても正方形で取りつくせず、隅にもとの長方形のパターンが繰り返し浮かび上がってきます。重箱の隅が何とやら！）

そのように、

「小数」：「連分数」（互除法）＝「循環する無限」：「有限」＝「循環しない無限」：「循環する無限」

と、きれいに一段シフトする対応が見られます。（「＝」や「：」の記号は、ここだけの厳密ではない使い方なのでご注意ください）。

同じものを、表現を変えることで、無限から有限に置きかわったり、また無限でも循環しないそれから循環するそれへと置きかわっています。とても興味深いことだとは思われませんか？！

さて、そこでまた興味が湧いてくることには、連分数展開して「循環しない無限」になるような数とは、一体どんな数なのでしょうか。

その数は、『虚数の情緒』を読み進めていくうちに、「真打」として登場します。