『ユークリッド幾何』 (担当:福西亮馬)
『私はピラミッドを建てた、という思い出を!』
今学期は、比例や相似をかいつまんで説明した後、ユークリッド『原論』第5巻(比例)の命題16、17と、第6巻(相似)の命題2、3、5、17、31の中から数問を選んで証明してもらいました。前学期は奇数偶数や素数の問いを見てきたので、久々に図形に戻ります。まずは道具となる定理を手に入れましょう。
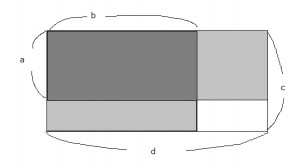
a:b=c:d ⇔ ad=bc
両端の積が真ん中の積になるという比較的覚えやすい、中学生で習う公式です。ただそれを納得して使えるように、自分たちでもオリジナルに証明してもらいました。代数的に考えると容易なのですが、幾何学的に表すと右の図のような意味を持ちます。
さてそれを道具として、第5巻にある命題で腕慣らしをした後、第6巻にある相似図形についての定理を証明していきました。今回はその中から代表して、命題2に挑戦中のA君の証明(途中まで)をご紹介します。
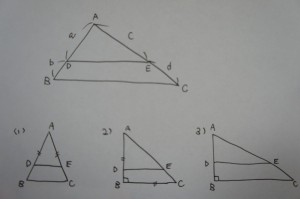
第6巻命題2
「三角形の一辺に平行な直線は他の二辺を等しい比に分かつ」
(線分DE//BCならば、AD:DB=AE:EC(a:b=c:d))
A君はよく見当をつけるために、イメージしやすい特殊な場合で解いた後、だんだんと条件を緩めていき、最終的に一般的な場合を証明するといった手法をとります。今回も、以下のようなステップを踏んでいました。
1)AB=ACという二等辺三角形
2)AB=BC、∠B=90°という(AB=ACではない)直角二等辺三角形
3)∠B=90°という直角三角形(条件AB=BCを外す)
4)任意の三角形
そしてA君は目下4)を考えており、以下は3)までの証明です。(紙面の都合で概略のみとしています)
A君の証明(概略)
1)AB=ACより、a=c、b=d。よってad=bcすなわちa:b=c:dが示せた。
2)点Dから線分ECに平行な線分を引き、DFとする。
するとEC=DF=b、DE=FC=a。
またAB=BC=a+bより、BF=BC-FC=a+b-a=b。
三平方の定理より、d2=DF2=DB2+BF2=b2+b2=2b2。
また同様に、c2=AE2=AD2+DE2=a2+a2=2a2。
よって、(ad)2=a2・2b2=2a2b2、
(bc) 2=b2・2a2=2a2b2。
ゆえに、(ad)2=(bc) 2となり、ad=bcが示せた。
3)2)と同様に考える。
ただし、△ADEと△DBFは相似なので、DE=ka、BF=kbとおける。
三平方の定理より、c2=AE2=AD2+DE2=a2+k2a2=(1+k2)a2、
d2=DF2=DB2+BF2=b2+k2b2=(1+k2)b2。
よって、(ad)2=a2・(1+k2)b2=(1+k2)a2b2、
(bc) 2=b2・(1+k2)a2=(1+k2)a2b2。
ゆえに、(ad)2=(bc) 2となり、ad=bcが示せた。
上の証明で、A君が直角三角形という特殊な条件を置いたのは、「三平方の定理が使えるかもしれない」というひらめきからでした。(またその定理を使うために引いた補助線が素晴らしいと思います)。
三平方の定理はこのクラスですでに証明済なので、もちろん使ってもよい道具です。ただし一つだけ注意点は、それを使うと2乗の計算が多く現れて式が複雑になることです(学校ではまだそれほど習っていないところです)。そこでA君はa2+k2a2の項が出てきた時に面食らって、自分が間違っているのではないかと思って悩んでいました。しかし後でそれが(1+k2)a2と一つにくくれることを見つけました。そして3)が2)をk=1の場合として含むことに気付き、2)を拡張してくれたのでした。
しかし、そのような一歩ずつのA君の証明を見て、ある方は、次のようなもっとシンプルな方法を提示されるかもしれません。
a:a+b=c:c+d ⇔ (a+b)・c=a・(c+d) ⇔ ac+bc=ac+ad ⇔ bc=ad ⇔ a:b=c:d(Q.E.D.)と。
これに対しA君は、まだ命題6.2の完全な証明(Q.E.D.)には至っていません。そこで次のような疑いがもたげて来るかもしれません──もしかしたら任意の三角形の場合には通用しない方法にこだわっているのではないか、と。さてここで、A君には今すぐ三平方の定理を使うことをやめて、スマートな方法に乗り換えた方がいいと勧めたものでしょうか。
私の答は、もちろん「No」です。A君の取った道はまだ先をたどることができます。たとえば、任意の三角形は2つの直角三角形に分割できることに着目すれば、三平方の定理を「2回」使うことで、3)はさらに拡張できます。もしA君がそれを思いついたなら、「任意の三角形の場合の三平方の定理」という、新たな収穫が得られることでしょう(それも高校で余弦定理を習う以前に!)。
このように、ある定理を証明しようとして有益な副産物が得られることは、実際に数学そのものの発展してきた道でもあります。それは、『フェルマー予想』など未解決問題の歴史を見てもうなずけます。ですので、A君が一般の三角形の場合の考察を終えてQ.E.D.と書き込んだ時、それはA君にとって「私はピラミッドを建てた」とも言える経験になることでしょう。
(なおフェルマー予想は、n=4の場合、n=3の場合、14、7、100以下の素数…と次第に包囲されて、とうとう解決に至ったわけですが、そのように特殊な条件を置くことはプロの数学者も使う常套手段です。そしてA君も何ら変わないと感じました。)
そして私が、未完成にも関わらず、なぜA君の上の証明を紹介したかと言いますと、それはA君の一歩一歩の手順が、「帰納的」だからです。もし私がスマートな方法を見せ、A君がそれを書き写して何か自信を得てくれたとしても、おそらくその自信はまたどこかで揺らいでしまうでしょう。一方、今ある数学は「彼が言った」(Dixit)ではなく「私が言った」(Dixi)の積み重ねによるものです。その数学そのものがたどってきた道のりを、自分の足でリアルに知的に進んでいるA君に、どうして「遠回りだ」などと言うことができるでしょうか。むしろそれが「王道」なのです。曲がりくねり、自分で歩いた部分こそが。
さて、私たちが『原論』を今も昔と変わらずに読むことができるのは、「A>B、B>C、ゆえにA>C」といった論理が普遍性を保っているからですが、この論理的構造は、いわゆる無形の金字塔です。それは古いから立派なのではなく、それ自身の生命力で立っていればこそです。実際、これほど長生きであるものに着手することに、どうして私たちは躊躇しなければならないことがあるでしょうか! ぜひ一緒に自分自身の手による証明を残し、有意義なピラミッド「群」を建てようではありませんか。Ergo, Exigamus!(だから、やり遂げよう!)
(福西亮馬)