福西です。こちらは前稿の内容の補足になります。クラスの様子とは特に関係がないです。ご興味のある方だけお読みください。
4294967297は、ある法則に基づいた数だと書きましたが、これは、
(2^2^n)+1
で、n=5を入れた時の数です。
このタイプの数には、フェルマー数という名前が付いています。実際にフェルマーが「素数を作り出すような公式はないか?」と考えて提案した式です。
残念ながら、
2^1+1=3
2^2+1=5
2^4+1=17
2^8+1=257
2^16+1=65537
までは素数なのですが、次の
2^32+1=4294967297
は、素数ではありません。(オイラーが最初に指摘)
素数の奥深さがうかがえる一つの例となっています。
フェルマーが考えた(2^2^n)+1は、素数の生成式ではなかったのですが、「じゃあそれ以降のフェルマー数で素数になる場合とならない場合はどうなっているのか」というのが、また別の興味深い話題ともなっています。(今のところn=4(65537)以降のフェルマー数に、素数は見つかっていません。またそれが本当にあるのかどうかも、まだ分かっていません)
<おまけ>
(2^2^n)+1の続きを確かめてみました。
n=5の場合
(2^2^5)+1
=2^64+1
=18446744073709551617
は、
=274177×67280421310721
に分解できます。(ともに素数です)
n=6の場合
2^128+1
=
3402823669
2093846346
3374607431
768211457
=
5964958912
7497217
×
5704689200
6851290547
21
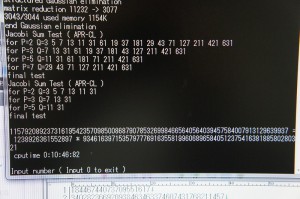
n=7の場合
2^256+1
=
1157920892
3731619542
3570985008
6879078532
6998466564
0564039457
5840079131
29639937
=
1238926361
552897
×
9346163971
535797776
9163558199
6068965840
5123754163
8188580280
321
確かに、合成数になっています。
(数字が長すぎて画面の表示から切れてしまうので、折って表示しています)
個人的には、ここまで見て、「二つの素数」に分解されているのが面白いと思いますが、この後も必ずそうなるかどうかは、私には分かりません(^^;)
なお、フェルマー数は、「ある数が作図可能かどうか」(コンパスと、目盛のない定規だけで作り出せる長さかどうか)という問題にも深く関係しています。ガウスが正17角形を描いて、その後、それを見抜きました。もし興味のある方は、ご自分でも、お調べになってみて下さい。
<参考>
・桁数無制限電卓(表示が省略されない電卓)
http://www.cybersyndrome.net/rsa/calculator.html
CtrlCとCtrlVを使って、4294967296(=2^32)を2回欄の中にペーストすれば2^64が計算できます。
それを繰り返せば、2^128も計算できます。(注意:ただしフェルマー数はそれに1を足した数です)。
だいたい桁数は倍ずつになっていきます。
この電卓で、下で求めた素因数分解の検算もできます。
・素数判定(素因数分解)プログラム
http://www.vector.co.jp/soft/dl/win95/edu/se059066.html
ダウンロードしたファイルfactor.exeを実行し、桁数無制限電卓で求めた数字を打ち込みます。(CtrlVが使えないので、手入力が大変ですけど^^;。でも↑キー(PgUp)で前の入力に戻れるので、打ち間違ってもすぐに直せます)
このプログラム、windows95用ですが、window7でも動きます。すごいです。扱える桁数が。
「このプログラムでの処理時間の目安は、Pentium 200Mで
50桁で 数分
60桁で 15分
70桁で 4時間
80桁で 35時間
90桁で 250時間」
で、
「100桁で3か月強(予想)」
だそうです。(READMEより)
ただ上の目安は10年近く前のスペックでの話なので、今のパソコンなら、もっと早いと思います。ちなみに上で求めたn=7のフェルマー数は78桁ですが、私のパソコン環境では10分で出てきました。