
『ユークリッド幾何』 (担当:福西亮馬)
『Q.E.D.!』
なぜ「幾何学なのか?」と問われれば、それはおそらく数学にとどまらず、物理学をはじめ、工学、哲学、さらに虚学、実学という垣根を越えて、さまざまな返答の仕方があると思います。
ただ私は単純に、「証明できることが楽しいから」という純粋な動機と、「ロボット工作において、プログラミングをする際に必要な論理性を磨けるから」という実用的な動機に駆り立てられてしています。みなさんはどうお考えでしょうか。
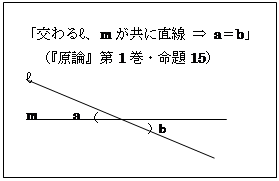 このクラスでは、ユークリッドの書いた『原論』の命題を、1回の授業で1つ選んで証明しています。最初に取り上げたのは、左にある命題でした。
このクラスでは、ユークリッドの書いた『原論』の命題を、1回の授業で1つ選んで証明しています。最初に取り上げたのは、左にある命題でした。
「交わるℓ、mが共に直線 ⇒ a=b」とは、「2本の直線が交わる時、その対頂角は等しい」ということの記号による翻訳です。この表現を見たとき、さっそくある生徒が「こういうのがまさに哲学的だと感じる」と意気揚々と申してくれました。なかなか面白い反応だと思いました。みなさんもぜひ一度解いてみて下さい。できればその「逆」(a=b⇒交わるℓ、mが共に直線)の証明にも挑戦してみて下さい。
さて授業では、まず平面上(2次元ユークリッド空間)で使える「定義」「公理」「公準」をかいつまんで説明し、その定義の中からただ一つ、「直線上の二点がなす角は180度(2直角)である」ことだけが、この問題では使える、というような制約を課しました。それだけで果して、この命題を証明することができるのでしょうか?
さっそく生徒たちは、果敢に頭を働かせ、知恵を絞って、この問題に挑戦してくれました。一人は周りに円を描いて「回転」させることで、また一人は長方形を描き加え、さらにもう一人は「折り返す」という方法で考えていました。
この手の問題の難しさは、見たままの直観に訴えられない(むしろそのことが誤りに導く)ことです。私がよく使う言い方では、「言葉の分からない宇宙人でも分かるように」、「中身の論理」で説明することです。ただし、すでに小学生の時に知っている「三角形の内角の和が180度である」ことも、「二等辺三角形の底角は等しい」ことも、残念ながらまだ自分たちで証明していないので、今は使えません。それらの「道具」は、これから一つずつじっくりと、自分たちの頭の中のフィルターを通して、ノートに書き加えていく予定です。もちろんそこに書かれていれば、自由に使ってよいことになります。そのような制約つきのプロセスを、「魔法使いの呪文書」にたとえてくれる生徒もいました。証明を一つする前と後との自分は、確かに一つの呪文を覚えているか否かのように、決定的な違いがあります。そのような「昨日とは違った自分」を発見できることは、これからもじわじわと楽しみになっていくことでしょう。
実際、授業で感心することは、生徒たちが誰一人、途中で問題を投げ出さないことです。「まだこうやったら解けるかも!」という希望を持って、途中の新たな発見を逐一、順番待ちをしながら、私にたずねてきます。「これはこうなって、こうなると考えたのですが、ここまでは合ってますか?」と。その時の彼らの論理的な説明は、非常に卓越したものがあると私は感じます。実際時間は80分なのですが、気がつくと2時間近く付き合っていることもあります。それはロボット工作の時とはまた質の異なる集中力です。それはただ「もし解けたら、きっとすごいことだぞ!」という純粋な欲求であり、最後に「Q.E.D.」と書くことを夢見てのことなのだろうと思います。
(福西亮馬)