福西です。「その2」からの続きです。
まずは適当にx=10として、歩数が3と10の場合を考えました。
52=40+12(=10×4+3×4)なので、可能。
53=50+3なので可能。
よって、3と10歩の場合は「可能」。
(ここで「可能」とは、51段以上のどんな段数がゴールであっても、3とx歩の組み合わせでぴったりゴールできることを意味します)
次に大まかに今度はx=20を考えました
52=20+20+12なので、可能。
53=20+33=20=3×11なので、可能。
よって、3と20歩の場合も「可能」。
次は、x=40の場合です。ここまで来るとすべて「可能」だと思えてきますが、実は「不可能」でした。
52=40+12なので、可能。
53は、どうやっても不可能。(なぜなら、13も53も、3の倍数ではないから)
よって、3と40歩の場合は、「不可能」。
(ここで「不可能」とは、51段以上について、「いつでもぴったりゴールできるとは限らない」という意味です)
そこで、次に興味を持ったのが、次の二つの点です。
A)10と20の間を埋めること
B)20から40の間で、可能な限界はどこか?
ここで私が、K君とY君を偉いなと思ったのは、このように次の疑問が出てきても、それを放っておかないことでした。実際、時間はだいぶ迫っていたので、「そこで終わり」とする選択肢もあったのですが、むしろ私が制止するのを振り払うような勢いで、自分たちでその疑問を包囲し始めたのでした。このように、先生が言ったからではなくて、自分たちが気になるから調べる、という意気込みには、体の大きさは関係なしに、頭が下がります。
さっそくK君はAの問題について、Y君はBの問題について、手分けして取りかかりました。
K君の調べた結果
3歩のペアとなるxが「3の倍数以外」なら、すべて可能だった。
つまり、x=10、11、13、14、16、17、19は可能で、x=12、15、18は(3歩とかぶるので)不可能。
Y君の調べた結果
3の倍数以外のx=20、22、23、25、26は可能。でも27、28は不可能。そしてそれ以降の40までが不可能。
この二人の結果を合わせると、次のようになります。
3の倍数以外で、x=10~26までは可能で、27~40は不可能。
ここで、次の疑問がまた出てきました。なぜ「26が限界なのか?」ということです。あるいは「40以降についてもすべて不可能か?」ということです。(もし26が可能と不可能の境界なら、40以降は不可能だということが示せます)。
二人は次のように考えてくれました。(以下その道筋)
26の次は28。まずは具体的にこの数について考えてみる。
3と28で、52と53の両方が作り出せればよいが、それは不可能。
なぜなら、52、53から28をのぞいた数を考えてみる。それらは24と23。
24は3で作り出せる。けれども23は3だけでは作り出せない。
なぜなら、この場合に条件を満たそうとすると、他に相方の歩数がいるが、あいにくそれが28と大きすぎるから(28>23)、不可能。
同様に、x>28についても、52と53は3とxでは作り出せない。
なぜなら52と53は連続した数なので、どちらかが3の倍数ならもう片方は3の倍数ではないから。
よってx=26が限界。
そしてこの26自体は、少し特殊である。
なぜなら、26は52のちょうど半分。つまり、52-26=26だから。
このため、たまたま、26は3の倍数ではないが、52=26+26として52段にぴったり止まれる。(なので可能)。
53-26=27。これは3の倍数。よって53段は可能。
よって、x=26は可能。
結論
「51段以上のグリコでは、3と、26以下の3の倍数でない歩数の2種類の歩数であれば、どんな段数でもぴったりゴールできる」
そんなこんなを考えてくれて、あっという間の1時間でした。
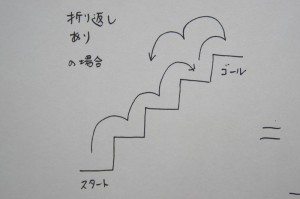
ちなみに他の問題設定として、「折り返しあり」(「その1」の問題2))の場合も、残り数分の間に考えてくれて、そちらでも大変面白い発見がありました。
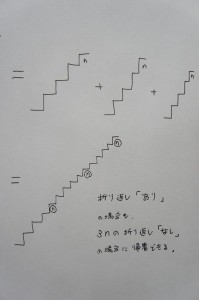
この図の意味するところは、折り返し「あり」 にした場合であっても、結局、段数を3倍に伸ばした場合の折り返し「なし」に帰着できるという事実です。(ゴールで止まらなかったら、戻って、また行ってとするわけなので、ゴールまでの道のりを3倍にした場合を考えていることになります。それでもゴールに止まらなければ、往復を追加して、5倍、7倍…としていけばいいわけです)
この発見から、仮に段数が、設定した歩数よりも小さかったとしても、段数を3倍、5倍…とすることで、段数の方を十分大きくすることができます。
そしてその段数が51を越えるようにすれば、先の問題で考えたことがそのまま適用できます。
そのような発見だけでも十分すごいなと思うのですが、しかしもっと、事を簡単にとらえられることを、K君がひらめいてくれました。
ここでは、使える歩数の種類はただ1種類だけとします。つまり、1歩ずつ、2歩ずつ、3歩ずつ、・・・y歩ずつと、進んでいくことを考えて、yがどのような数なら、ぴったりゴールできるかを考えます。
K君が考えてくれたのは、3歩の場合です。それは、
「段数が3倍になっている時点で、段数は3の倍数である」
ということでした。K君は続けます。
「つまり、3歩ずつであったら、段数がどんな場合でも、行って→帰って→行って、で必ずぴったりゴールできる」
と。
なるほど!
その通りです!
この発見には私もびっくりしました。ということは、その議論を押し進めて、5歩ずつなら往復を伸ばして段数を5倍にすれば、また7歩ずつなら7倍にすれば可能だということになります。(任意の奇数歩で可能であることが言えます!)
さらに、任意の偶数歩の場合でも、次のように考えれば解決です。
(K君は「行って帰って行って、行って帰って行って、を繰り返す」と表現していました)
普通に往復を増やすだけでは、2倍ずつ増えるので、段数は1倍→3倍→5倍・・・と、奇数倍にしかなりませんが、その奇数倍をさらに偶数倍を繰り返すことはできます。
たとえば、段数を6の倍数にしたい時は、30倍(5×6)まで段数を増やせばいいことになります。
そうすれば、yが奇数の場合でも偶数の場合でも、つまり、どんな場合でも成り立つことが言えます!
結論
折り返し「あり」の場合のグリコの問題では、どんな段数に対しても、任意に設定した1種類の歩数で、必ずぴったりゴールできる。
以上、いろいろと発見があって、この日は豊作でした。